Note
The Golden Ratio is also equal to 2 × sin(54°), get your calculator and check!
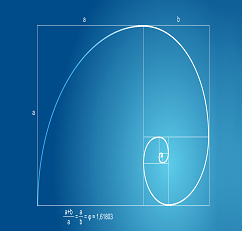
In mathematics, two quantities are in the golden ratio if their ratio is the same as the ratio of their sum to the larger of the two quantities. The figure illustrates the geometric relationship. Expressed algebraically, for quantities a and b with a > b > 0,

The Golden Ratio is also equal to 2 × sin(54°), get your calculator and check!
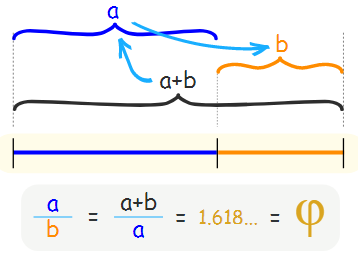
Putting it as simply as we can, the Golden Ratio (also known as the Golden Section, Golden Mean, Divine Proportion or Greek letter Phi) exists when a line is divided into two parts and the longer part (a) divided by the smaller part (b) is equal to the sum of (a) + (b) divided by (a), which both equal 1.618. But don’t let all the math get you down. In design, the Golden Ratio boils down to aesthetics— creating and appreciating a sense of beauty through harmony and proportion.
Phi can be defined by taking a stick and breaking it into two portions. If the ratio between these two portions is the same as the ratio between the overall stick and the larger segment, the portions are said to be in the golden. You can also think of phi as a number that can be squared by adding one to that number itself, according to an explainer from mathematician Ron Knott at the University of Surrey in the U.K. In fact, our brains are seemingly hard-wired to prefer objects and images that use the Golden Ratio. It’s almost a subconscious attraction and even tiny tweaks that make an image truer to the Golden Ratio have a large impact on our brains. Take a square and multiply one side of by 1.618 and you will get a rectangle of harmonious proportions. Now, if you lay the square over the rectangle the two shapes will give you the Golden Ratio. If you keep applying the Golden Ratio formula to the new rectangle, you will eventually get diagrams with progressively smaller squares.
Whoa! Need a break? Hold on, just a few mind-bogglers to go. If you take the Golden Ratio diagram above and draw an arch in each square, from one corner to the opposite corner, you will draw the first curve of the Golden Spiral (or Fibonacci Sequence) – a series in which the pattern of each number is the sum of the previous two numbers. Starting at zero, the sequence is: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144… and so on. By adding the arch in each square, you’ll end up with the diagram of the Golden Spiral. The squares of the edges of this triangle are also in geometric progression according to the golden ratio itself. Some sources claim that a triangle with dimensions closely approximating a Kepler triangle can be recognized in the Great Pyramid of Giza, making it a golden pyramid.

In book 6 of The Elements, Euclid gives us the definition of the Golden Ratio.
He instructs us to take a line segment and divide it into two smaller segments such that the ratio of the whole line segment (a+b) to segment a is the same as the ratio of segment a to segment b, the way it is shown in this example. Golden Ratio is used to determine the size of and placement of each element to ensure a well-proportioned cover. The Golden Ratio can be applied to shapes too.
The golden ratio occurs in many mathematical contexts. It is geometrically constructible by straightedge and compass, and it occurs in the investigation of the Archimedean and Platonic solids.
One very famous piece, known as the Mona Lisa, painted by Leonardo Da Vinci, is drawn according to the golden ratio. The Mona Lisa is one of the most valuable paintings in the world. It holds the Guinness World Record for the highest known insurance valuation in history at US$100 million in 1962. The golden ratio is 1:0.618 and has been coined golden because it is said to be aesthetically pleasing. A golden rectangle is simply a rectangle with dimensions that reflect the golden ratio. The Mona Lisa has many golden rectangles throughout the painting. By drawing a rectangle around her face, we can see that it is indeed golden.
The rectangle shown has been made using the Golden Ratio, looks like a typical frame for a painting, doesn't it? It can be positioned and the rectangle will always be in golden ratio.
Two quantities a and b are said to be in the golden ratio φ if:
(a+b)/a=a/b
Ancient Greek mathematicians first studied what we now call the golden ratio, because of its frequent appearance in geometry the division of a line into "extreme and mean ratio" (the golden section) is important in the geometry of regular pentagrams and pentagons. Euclid's Elements provides several propositions and their proofs employing the golden ratio, and contains its first known definition which proceeds as follows:
"A straight line is said to have been cut in extreme and mean ratio when, as the whole line is to the greater segment, so is the greater to the lesser."
Let's see a example where the spread of a scale can be changed and A:B will always be in golden ratio.